Description
By default, a Delaunay based method is used to insert points into an unstructured domain when it is initialized. Alternatively, you may select the Advancing Front, Advancing Front Ortho, or Thin Surface Interpolation methods.
The Algorithm pull-down provides a choice of four methods for filling the isotropic portion of the domain:
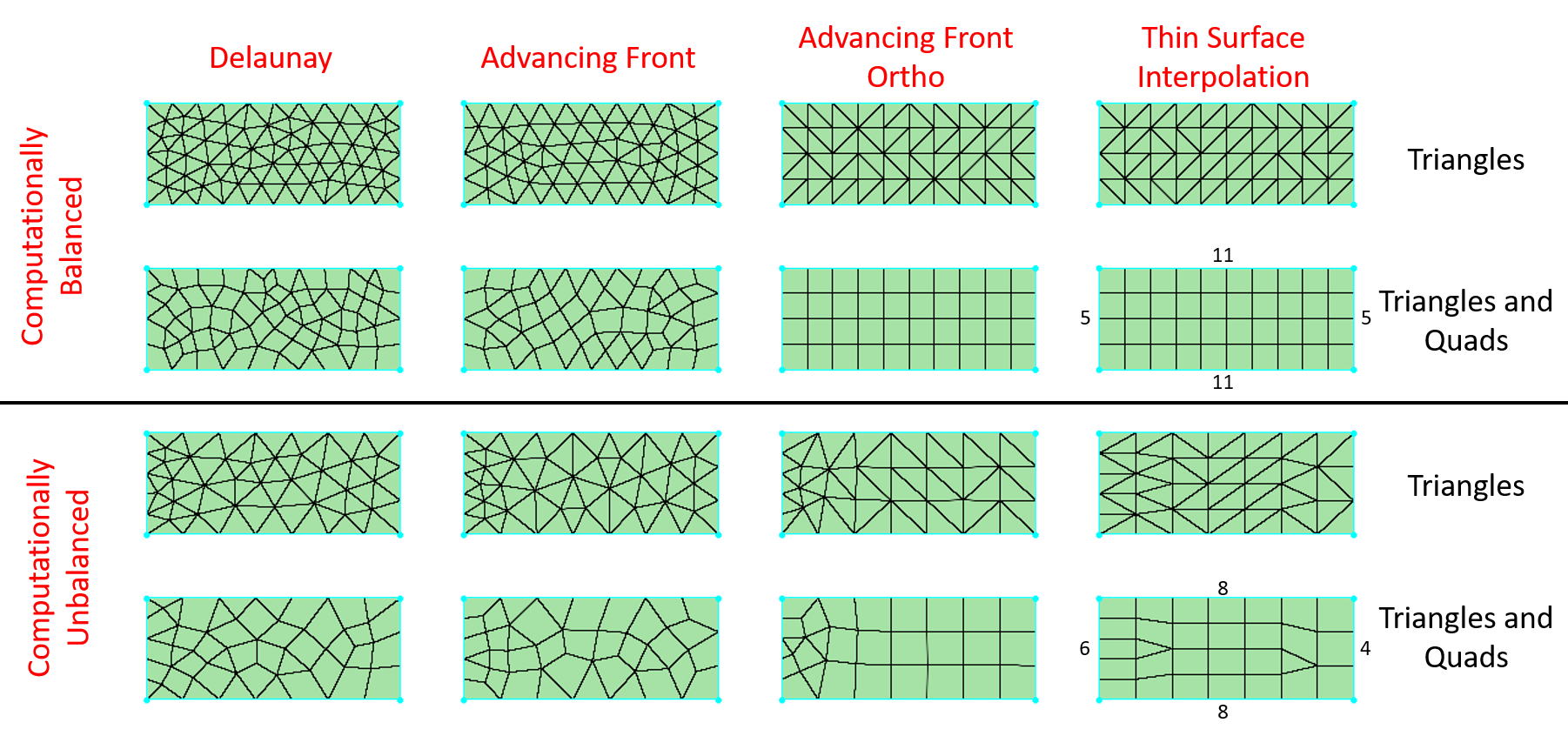
- Delaunay: Fills the interior of the domain with isotropic cells (triangles or triangles and quads) using a modified Delaunay approach. Delaunay is the default option for Algorithm.
- Advancing Front: Fills the interior of the domain with isotropic cells (triangles or triangles and quads) using an advancing front approach. When Cell Types is set to Triangles, Advancing Front produces equilateral triangles that are more uniform in appearance than Delaunay.
- Advancing Front Ortho: Fills the interior of the domain with right-angled isotropic cells (triangles or triangles and quads) using an advancing quad approach.
- Thin Surface Interpolation:
Fills the interior of the domain with cells (triangles or triangles and quads)
with a more structured-like appearance than can be achieved using Advancing Front or
Advancing Front Ortho, without strictly requiring the domain to be
computationally balanced or linked to a structured domain.
Thin Surface Interpolation is intended to be used on long thin rectangular surfaces (such as the blunt trailing edge of a wing), where using diagonalized structured domains is not possible or practical. Similar to structured domains, T-Rex is not available for domains using Thin Surface Interpolation and source influence only affects the spacing distribution on the bounding connectors.
Caution: Since Thin Surface Interpolation is intended as an alternative to structured domain initialization, the attributes in the Cells frame, Quads frame, T-Rex tab, and Size Field tab have no impact. However, these attributes are used with the Advancing Front Ortho algorithm if Thin Surface Interpolation fails due to one of the constraints below.
Additionally, Thin Surface Interpolation can only be applied to domains that meet certain constraints, otherwise the algorithm defaults to Advancing Front Ortho and a warning message is printed to the Messages window. Please click the Thin Surface Interpolation Constraints button below to view a table listing the constraints and their meanings.
Message Meaning Too many edges The definition of the unstructured domain has more than 1 edge. Thin Surface Interpolation is not supported for domains that contain interior edges. Edge must contain at least 4 connectors The domain is not defined by at least 4 connectors. Could not identify 4 suitably concave corners at nodes The loop of connectors defining the domain does not contain 4 nodes that can be identified as distinct corners (i.e. the angle is between 18 and 162 degrees). Could not identify a unique short side The sides of the domain must not be equally dimensioned. The preferred configuration is high-low-high-low. Folded cells detected The domain cannot contain folded elements. You can use Edit, Curve to check that the bounding connectors do not contain folds in their underlying definitions.
The figure below shows a comparison of the grid characteristics produced by the four algorithms using both the Triangles and Triangles and Quads cell type options. Note the differences between the Advancing Front Ortho and Thin Surface Interpolation algorithms when using computationally unbalanced domains.