Fidelity Pointwise Grid Types

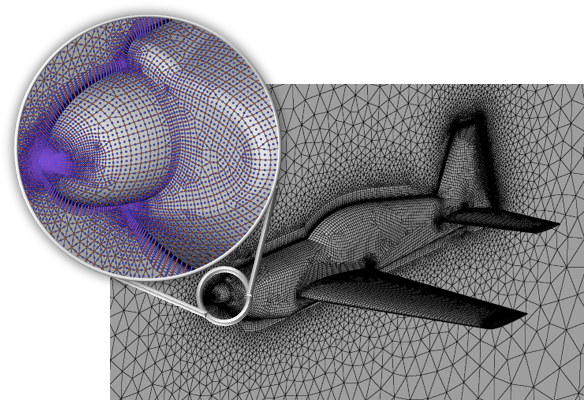
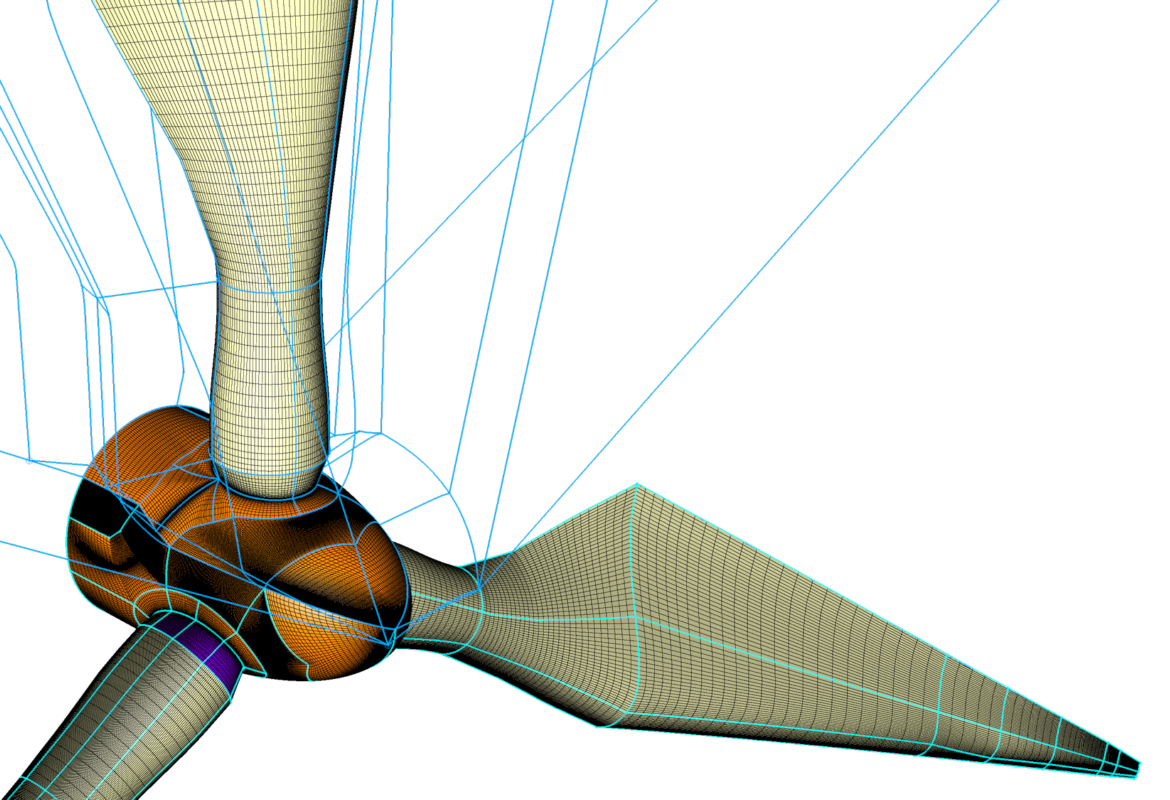
Description

Fidelity Pointwise generates structured, unstructured, hybrid, overset, voxel, and high-order grids. The element types it makes include triangles, quadrilaterals, tetrahedra, pyramids, prisms and hexahedra. Fidelity Pointwise divides the overall computational space into one or more sub-regions called blocks.

Fidelity Pointwise can be used to generate both 2D and 3D blocks. A 2D block consists entirely of surface cells while a 3D block contains entirely volumetric cells. All blocks in the same grid must either be 2D or 3D; you cannot combine blocks of differing dimensionality in the same grid.

Tip: When deciding which topology to use for a geometry, there are several factors you have to take into consideration: how much time you have available for the grid generation process, the grid types your solver supports, the accuracy desired in certain areas of your grid, and the desired grid size.

Structured, Unstructured, and Hybrid Grids

The type of each block can either be structured, unstructured or hybrid. A structured block consists entirely of quadrilateral (2D) or hexahedral (3D) cells that have been arranged in an ordered IxJxK array. An unstructured block consists of triangles and quadrilaterals (2D) or tetrahedral, pyramid, prism, and hexahedral cells (3D) having no implicit order. If all blocks in a grid are structured, then the overall grid type is called structured. When all blocks in a grid are unstructured, then the overall grid type is called unstructured. If the grid consists of both structured and unstructured blocks, the overall grid is called hybrid, a special type of unstructured grid.

This structured grid was generated using the Glyph scripting language.

This unstructured grid was generated using the T-Rex meshing algorithm.

Special Grid Types

Fidelity Pointwise can also be used to generate the following special grid types in 3D: overset, voxel, high-order.

Overset grids use multiple disconnected grids to discretize the computational space. The component grids (which can be structured, unstructured, or hybrid) need only overlap each other to completely cover the computational space and may intersect one another. As a final pre-processing step, a composite grid assembly software determines both which grid points lay outside the computational space and grid-to-grid connectivity.

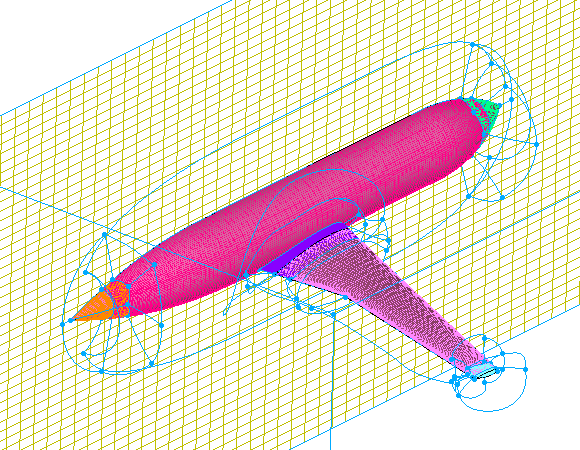
This overset grid was assembled using 7 overlapping structured component grids. The surface grid and symmetry plane have been colored according to which of the component grids they belong.

Voxel grids are a special type of unstructured grid that use layers of regular cartesian-aligned hexahedral cells, instead of isotropic tetrahedral cells, to fill the interior of the volume.

This voxel grid was created by using the T-Rex meshing algorithm to create the boundary layer and point cloud sources to give additional refinement below the rotors.

High-order grids provide increased solution accuracy for finite-element solvers by increasing the polynomial degree of the basis functions assumed for the solution within each element (also known as P-refinement). High-order grids are created from an initial linear (or P1) grid by increasing the number of points that define each element according to the desired polynomial definition (quadratic, cubic, etc.). As a final pre-processing step, the grid is deformed and smoothed in order to accurately capture curved geometry.

This high-order grid was created by elevating an unstructured grid to P2. The inset image displays the grid points on the surface and symmetry plane near the nose. Linear points are displayed in red and high-order points are displayed in blue.