Description
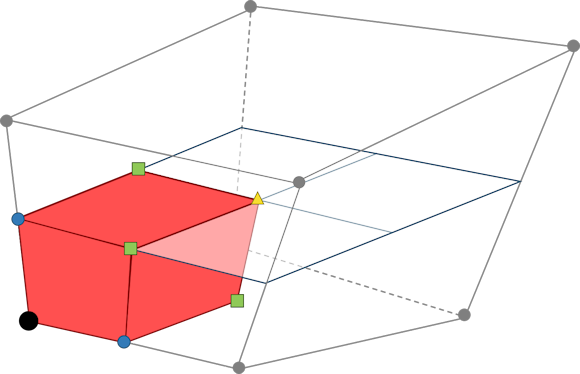
For blocks only, vertex-centered volume measures the volume of the control volume in the dual mesh centered around each grid point (i.e. volume cell vertex) in the block. This metric is computed by subdividing each volume cell into sectors using the cell's vertices, edge midpoints, face centroids, and volume centroid. The diagram below shows how one such sector is defined around one of the vertices of a hexahedral volume cell.
Tip: Use the probe functionality while in the Examine command to visualize the dual mesh control volume when examining any vertex-centered function.
This subdivision results in one hexahedral sector (shown in red) for each vertex in the volume cell regardless of volume cell type. The volume of the vertex's control volume is then computed by summing together the volume of each of its contributing sectors.
Note: A pyramid can be thought of as a hexahedron with one collapsed face. In the example diagram above, if you collapse the front face of the hexahedral volume cell, the corresponding face of the sector (shown in red) also collapses. The apex vertex of pyramids is associated with four collapsed hexahedron sectors, one from each vertex in the volume cell that collapsed to form the apex.
For this function, the probe renders the vertex and the bounding faces of the dual mesh control volume. Be aware that this metric may vary from the volume reported by your vertex-centered solver due to the fact that there are several different methods for defining the dual mesh.